Magnetic dipole moment or magnetic moment (often denoted by letter m or μ)¹⁾²⁾ - a vector quantifying the magnetic property of a current loop, equal to the product of the electrical current and the loop area. The direction of magnetic moment $\vec m$ is defined by the right-hand rule and is perpendicular to the plane of the loop.³⁾

This convention defines the polarity of magnetic poles, with the sense of the arrow denoting magnetic north pole.⁴⁾

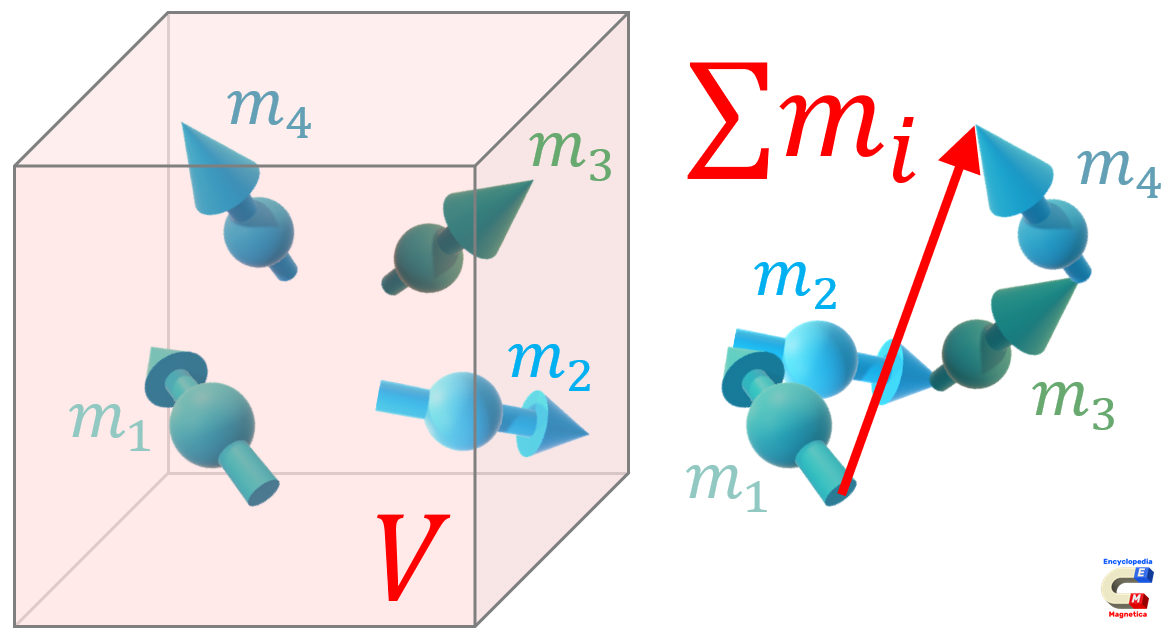
Magnetic dipoles are used as the basis for the definition of magnetisation M (response of matter to being magnetised).

Magnetic dipole moment $\vec m$ of a loop of current $\vec I$ with the loop area $A$ and unit vector $\vec a$ (normal to $A$)

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

The magnetic dipole moment is a product of the amplitude of the current $I$ and the area $A$ of the loop: ⁵⁾

The vector $\vec m$ is oriented in the same direction as the unit vector $\vec a$, normal to the surface $A$:

Magnetic moment is a pseudovector⁶⁾ and a force or torque acts on the “centre of mass” of the dipole.⁷⁾

The current loop is known as “magnetic dipole” because of the similarity of the character of the field to that of an electric dipole. In some cases, a similar logic can be applied for analysis of the fields and a magnetic dipole can be represented as a field of two hypothetical separated magnetic monopoles:⁸⁾

where: $p$ - strength of magnetic monopoles (A·m), $l$ - distance between the poles (m).

From theoretical viewpoint, the magnitude of magnetic moment, as a product of current and area, can remain constant when the area is shrinking and the current is increasing. In practice, when analysing atomic behaviour, at sufficiently large distance from the dipole the magnetic field is independent of the shape of the dipole, and the magnetic field distribution is identical to an infinitesimal, point-like dipole (see the animation below).⁹⁾

Magnetic flux density $\vec B$ associated with the current loop

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

Field lines around magnetic dipole
^{by Geek3 and S. Zurek, CC-BY-SA-3.0}

Field lines around magnetic dipole and electric dipole are similar (far from a dipole)
^{by Geek3, CC-BY-SA-3.0}

For distance much larger than the radius r of the current loop the magnetic field does not depend on the shape of the current loop, and can be calculated in spherical coordinates (for distance R and angle θ):¹⁰⁾

Uniform magnetic field B acts with a torque τ on the magnetic dipole m, tending to align m parallel to B

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

If the current loop is exposed to magnetic field, in the form of magnetic flux density (vector of B) then the magnetic moment allows calculation of the torque $\tau$, which will tend to align the current loop parallel to the applied B. This torque has an energy associated with it:¹¹⁾

The energy $U$ associated with a magnetic dipole moment m placed in magnetic field B is:^12)13)14)

Positions of lowest energy (parallel) and highest energy (anti-parallel)¹⁵⁾

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

The change in energy required to flip the dipole from the lowest energy position (magnetic moment parallel with the field) to the highest energy position (magnetic moment anti-parallel with the field) is:¹⁶⁾

A gradient of magnetic field B exerts a mechanical force F on a magnetic dipole m; in uniform field there is just torque and no force¹⁷⁾, i.e. there are local forces but their effects cancel around the whole loop (see also: compass)

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

The external magnetic field exerts the magnetic force on each infinitesimal part of the current loop. In a uniform parallel field the forces act only radially, so the net force on the dipole is zero.

However, if the current loop is placed in a gradient of flux density B then the magnetic dipole moment allows calculation of the force F which will attract or repel it, depending on the mutual alignment of the vectors of B and m.

For a general three-dimensional case:¹⁸⁾

where: $\nabla$ is the nabla operator.

The calculation simplified for a single axis x is:¹⁹⁾

Magnetisation M is a vector sum of magnetic moments per unit volume V of material, so $M = \sum{m} / V$, from which the sum of magnetic moments is $\sum{m} = M·V$. Therefore, knowing magnetisation of the sample and its volume it is possible to calculate the force acting on it due to the gradient of the applied magnetic field B or H, which in vacuum gives:²⁰⁾

The force exerted by a current loop, or a magnetic dipole a on b, separated by a distance R much larger than their radius, can be calculated by solving the following double integral:²¹⁾

where: $I_a$ and $I_b$ - currents in loop a and b, respectively (A), $\vec d_a$ and $\vec d_b$ - infinitesimal vector of the paths a and b, respectively (m), $\vec R$ - vector from $\vec d_a$ to $\vec d_b$ (m).

Diagram of two magnetic dipoles a and b, for calculation of force and torque between them²²⁾²³⁾

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

where: $m_a$ and $m_b$ are the magnetic dipole moments (A·m²), $\hat m_a$ and $\hat m_b$ are the unit vectors in directions of the dipole vectors, $\hat r$ is the unit vector along the direction from the centre of the a dipole to the centre of b dipole, $r$ is the distance between the centre of the dipoles (m), $\vec m_a$ and $\vec m_b$ are the dipole moment vectors (A·m²).

If the two moments are aligned on the same axis, then all the terms with vector cross products are eliminated, the force acts only on the axis, and the equations simplifies to:²⁴⁾

The magnetic field generated by the dipole a at the location of b is:²⁵⁾

The torque $\vec τ_{ab}$ exerted on a dipole b by magnetic field generated by the dipole a, separated by a distance R much larger than their radius is:²⁶⁾

which when evaluated gives:

where: $m_a$ and $m_b$ are the magnetic dipole moments (A·m²), $\hat m_a$ and $\hat m_b$ are the unit vectors in directions of the dipole vectors, $\hat r$ is the unit vector along the direction from the centre of the a dipole to the centre of b dipole, $r$ is the distance between the centre of the dipoles (m), $\vec m_a$ and $\vec m_b$ are the dipole moment vectors (A·m²).

In a general case, the torque exerted on b from a is not equal to the torque on a from b, but the total angular momentum of the system is conserved:²⁷⁾

Simplified illustration of the orbital magnetic moment $\vec m_o$ and spin magnetic moment $\vec m_s$²⁸⁾

^{S. Zurek, E-Magnetica.pl, CC-BY-4.0}

Sub-atomic particles such as electron, proton and neutron possess magnetic moments, which are inversely proportional to their masses, so the magnetic moment of electron is larger, because its mass is smaller.

There are two contributions to electron magnetic moment: the orbital magnetic moment (whose value is orbit-dependent ²⁹⁾) and the spin magnetic moment (often expressed as a ratio to the constant Bohr magneton).³⁰⁾

The magnetic properties of matter are dictated mostly by the magnetic moments of the electrons.³⁵⁾ Very strong magnetic effects (which are utilised in electromagnets, electric motors, transformers, etc.) require sufficiently dense packing of atoms in the matter, so the the spin-spin interactions can produce their long-range ordering, required for example for emergence of ferromagnetism.

• Electric charge
• Magnetic force
• Magnetic field
• Current loop
• Torque
• Nuclear magnetic moment